Параметрическая 3D кривая

Вызов команды:

Команда Параметрическая 3D кривая вызывает режим создания параметрических кривых, доступный в рамках общей команды 3D кривая. После вызова команды можно в любой момент переключиться в режим создания 3D кривых других типов с помощью выпадающего списка в разделе Тип в верхней части окна параметров команды. Полный список доступных типов приведён в описании команды 3D кривая.

Способ создания 3D кривой с параметрическим изменением 3D точки используется для создания траекторий со сложной геометрией.

Пространственная кривая получается в результате движения 3D точки по произвольной или специально заданной пространственной траектории. Движение точки осуществляется за счёт многократного копирования исходной 3D точки. Полученный набор точек объединяется сплайном и формируется 3D кривая. Результирующая 3D кривая может быть замкнутой.

При построении такой кривой используется универсальный механизм, позволяющий получать конечный результат на основе параметрического копирования исходного элемента. Этот механизм используется в операции «Тело по параметрам» – при создании тела на основе движения (копирования) профиля. Он же используется в операции «Параметрический массив», где результатом выполнения операции является набор параметрически изменяющихся копий исходного объекта.

Наиболее полно работа этого алгоритма описана в главе «Тело по параметрам». В данной главе приведено лишь краткое описание и некоторые примеры применения данного механизма.

Для создания 3D кривой с параметрическим изменением точки необходимо определить закон, по которому будут строиться копии исходной 3D точки.

Для каждой копии точки рассчитывается так называемая система координат текущей копии. Копирование 3D точки осуществляется в направлении от исходной системы координат к рассчитанной целевой системе координат текущей копии. В качестве исходной системы координат пользователь может выбрать одну из локальных систем координат модели. Если локальная система координат не выбрана, то в качестве исходной системы координат используется, в зависимости от способа расчёта системы координат текущей копии, либо глобальная система координат, либо система координат первой копии.

Система координат текущей копии (т.е. её начало и ориентация осей) может определяться одним из двух способов:

•Свободная ориентация копии. Законы изменения параметров системы координат текущей копии 3D точки описываются с помощью выражений.

•Ориентация копии по 3D кривым или поверхностям. Для определения положения в пространстве системы координат текущей копии используются существующие 3D кривые или поверхности других тел. Управляя системой координат копии, пользователь управляет положением каждой копии 3D точки.

Управление системой координат копии осуществляется через параметры операции. Параметры подразделяются на два типа - управляемые параметры и управляющие параметры.

Управляемые параметры – параметры, значения которых рассчитываются автоматически в процессе создания копии точки. Для считывания значений таких параметров можно назначить независимые переменные.

Управляющие параметры – поля, зависимости в которых задаются пользователем. В поля управляющих переменных вписываются произвольные выражения, в которые можно включить любую переменную системы. Например, если включить в такое выражение переменную, отвечающую за номер копии 3D точки, значение данного параметра будет зависеть от номера копии.

Некоторые параметры операции могут быть как управляющими, так и управляемыми. Ведущий параметр Номер копии всегда является управляемым. Для него обязательно нужно выбрать независимую переменную, которой будет присваиваться текущее значение номера копии при расчёте операции. Номер копии автоматически изменяется в процессе расчёта от 1 до указанного количества с шагом 1.

Расчёт выполняется в следующем порядке: присваивается следующее значение номеру копии, рассчитываются управляющие параметры, вычисляются остальные управляемые параметры (если они есть), выполняется копирование. Все полученные копии 3D точки объединяются в один сплайн.

 

После вызова команды становятся доступными следующие действия:

Как уже отмечалось выше, можно выделить два способа создания кривой с параметрическим изменением 3D точки. Рассмотрим на примерах каждый из них.

Способ свободной ориентации копии

При создании кривой таким способом достаточно выбрать 3D узел, задать количество копий и назначить независимую переменную на параметр Номер копии. Используя переменную, принимающую значения номеров копий, можно создать определённые зависимости в полях управляющих переменных, а также в 2D или 3D построениях, от которых, в свою очередь, будет зависеть положение исходной 3D точки.

Пример 1

Рассмотрим применение параметрической кривой на примере создания модели кулачка. Данный пример находится в библиотеке Примеры 18, в папке 3D Построения/3D Кривая/Кулачок.grb. Исходными данными является график, задающий поверхность кулачка.

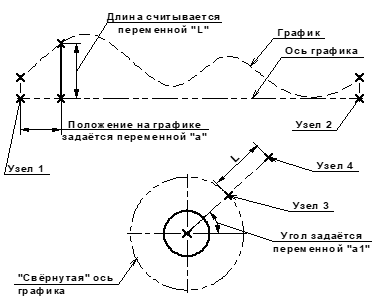
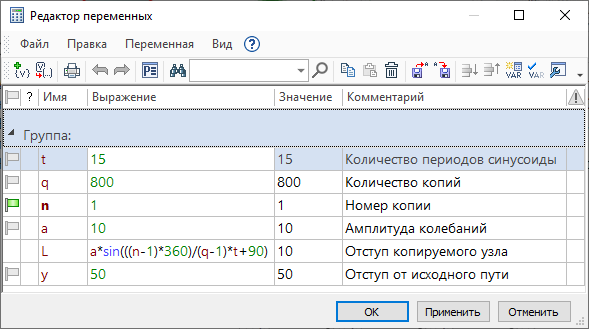
Между узлами 1 и 2 построена пропорциональная прямая. Её положение определяется значением переменной а в пределах от 0 до 1 включительно. При изменении значения переменной а прямая будет двигаться от точки 1 к точке 2. Полученная прямая пересекает ось графика и кривую графика. Между этими точками можно построить отрезок. Его длина будет равна текущему значению функции графика. Считанное (с помощью функции get) значение длины отрезка хранит переменная L.

Для построения 3D кривой, повторяющей контур поверхности кулачка, необходимо создать такой 3D узел, который бы при изменении одной переменной (назначенной на счётчик копий) изменял своё пространственное положение в соответствии с заданным законом на графике. Такой узел удобно создать, если добавить ещё несколько 2D построений с использованием уже полученных данных.

Для того чтобы получился кулачок нужных размеров, ось графика должна быть «свёрнута» в окружность заданного радиуса. В данном примере построена окружность радиусом 50 мм. Через центр окружности под углом к горизонтали нужно построить новую прямую. На параметр, задающий угол наклона этой прямой, нужно назначить переменную а1.

На пересечении окружности и наклонной прямой построен узел 3. Относительно узла 3, вдоль наклонной прямой построен узел 4 на расстоянии L. По 2D узлу 4 построен 3D узел. Для этого на существующей странице предварительно создана рабочая плоскость «Вид спереди».

Теперь нужно связать все переменные между собой таким образом, чтобы при изменении счетчика копий перестраивался 3D узел. Этого можно добиться, если вместо конкретных значений некоторых переменных ввести следующие выражения, задающие зависимость от номера копий.

Теперь нужно связать все переменные между собой таким образом, чтобы при изменении счетчика копий перестраивался 3D узел. Этого можно добиться, если вместо конкретных значений некоторых переменных ввести выражения, задающие зависимость от номера копий.

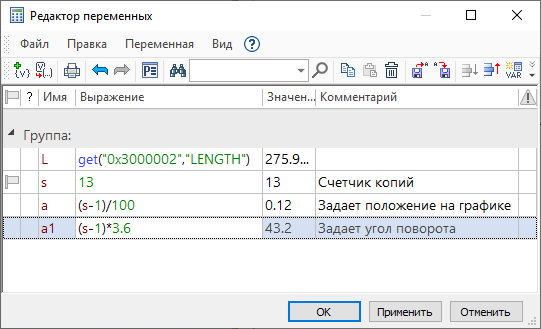
Поскольку значения параметра Номер копии всегда начинаются с единицы, иногда требуется вводить поправку (–1) в выражения, где участвует переменная Номер копии.

Теперь можно строить параметрическую 3D кривую. В диалоге параметров нужно определить два параметра: задать количество копий, и назначить переменную, которая будет выполнять функцию счётчика копий. В данном примере на параметр Номер копии назначена переменная s.

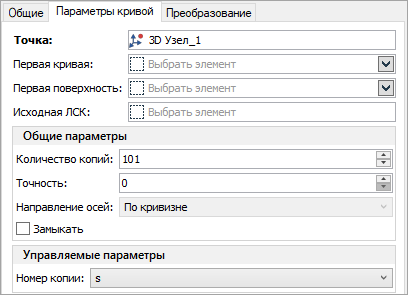
Первая копия 3D узла будет совпадать по положению со 101-й. В результате получится замкнутая 3D кривая. Её геометрия будет соответствовать форме кулачка.

Далее для получения тела кулачка нужно вытолкнуть кривую по нормали на 50 единиц и на основе получившейся поверхности создать твёрдое тело с помощью операции «Сшивка».

В завершение можно сделать цилиндрическое отверстие по оси кулачка (выталкивание окружности с автоматическим вычитанием из основного тела).

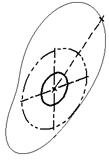
Способ ориентации копии по кривым или поверхностям

Способ ориентации копии по кривым или поверхностям удобно использовать, когда не удаётся точно описать закон изменения параметров копии с помощью выражений. В таких случаях бывает удобно использовать различные 3D кривые или поверхности для определения положения и ориентации системы координат текущей копии.

Пример 2

В качестве примера применения параметрической 3D кривой с ориентацией копии по кривым или поверхностям можно рассмотреть построение 3D кривой, определяющей внешний край «волнистой» поверхности. На рисунке ниже она обозначена цифрой (2).

Для построения такой кривой необходимы:

•исходный 3D узел, положение которого должно меняться при создании кривой в зависимости от номера создаваемой копии;

•3D кривая, определяющий положение начала системы координат каждой копии;

•поверхность, определяющая ориентацию оси X системы координат каждой копии.

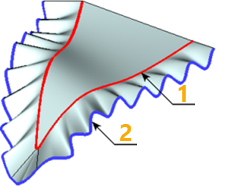
Создаваемая кривая должна повторять форму внешнего края исходной поверхности. Поэтому для задания начала системы координат копий необходимо использовать 3D кривую, построенную по рёбрам исходной поверхности. На рисунке выше она обозначена цифрой (1).

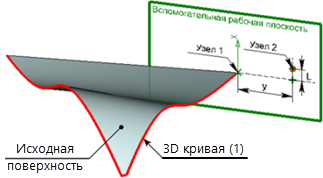
Для получения исходного 3D узла построена вспомогательная рабочая плоскость, перпендикулярная кривой (1) и проходящая через одну из вершин исходной поверхности.

На рабочей плоскости созданы необходимые 2D построения. Искомый 3D узел создан по 2D узлу на рабочей плоскости – Узлу 2.

Узел 2 был построен следующим образом: на рабочей плоскости построен Узел 1 с координатами (0,0) (соответствует той вершине исходной поверхности, через которую проходит рабочая плоскость). Через данный узел проведена горизонтальная прямая.

Перпендикулярно горизонтальной прямой, на расстоянии y от Узла 1, проведена вертикальная прямая. Узел 2 лежит на данной прямой на расстоянии L от точки пересечения прямых.

Значение переменной L задано так, чтобы оно менялось при изменении счётчика копий 3D кривой. Таким образом, при построении 3D кривой, в зависимости от номера текущей копии по синусоидальному закону меняется положение 2D Узла 2 и построенного на его основе 3D узла.

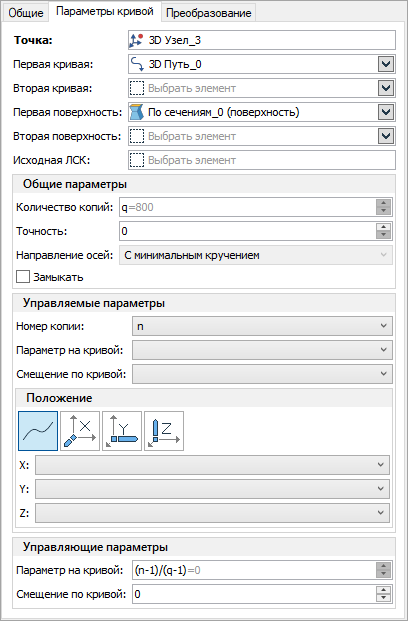
Для задания ориентации оси X системы координат копий при построении параметрической кривой необходимо указать саму исходную поверхность. Если поверхность не выбирать, то ориентация осей будет определяться на основе вектора кривизны 3D кривой (1), направление которого может резко меняться.

В диалоге параметров кривой нужно определить: количество копий (переменная q), переменную-счётчик копий (в данном примере это переменная n) и управляющий параметр Положение на кривой.

Когда 3D кривая (2) создана, можно построить на её основе «волнистую» поверхность с помощью операции «По сечениям».

Данный пример находится в библиотеке Примеры 18 в папке 3D Построения/3D Кривая/Параметрическая кривая с ориентацией копий по кривой и поверхности.grb.

См. также:

•3D кривая

•Обрезка 3D кривой по точкам

•Проекция 3D кривой